Autoregressive Processes
Autoregressive process 란 history 가 현재 값에 직접적인 영향을 주는 time series 를 말한다. 식으로 표현하면 아래와 같다.
현재시점 (t) 의 값은 과거 시점들 (t-1 ~ t-p) 의 값을 가중치를 두고 합한 값에 error term (Z) 을 더한 값이다.
$$ X_t = Z_t + \phi_1(X_{t-1}) + \phi_2(X_{t-2}) ... + \phi_p(X_{t-p}) $$
Example
p=2 이고, 가중치가 0.7, 0.2 인 autoregressive process 는 아래와 같다.
$$ X_t = Z_t + 0.7X_{t-1} + 0.2X_{t-2} $$
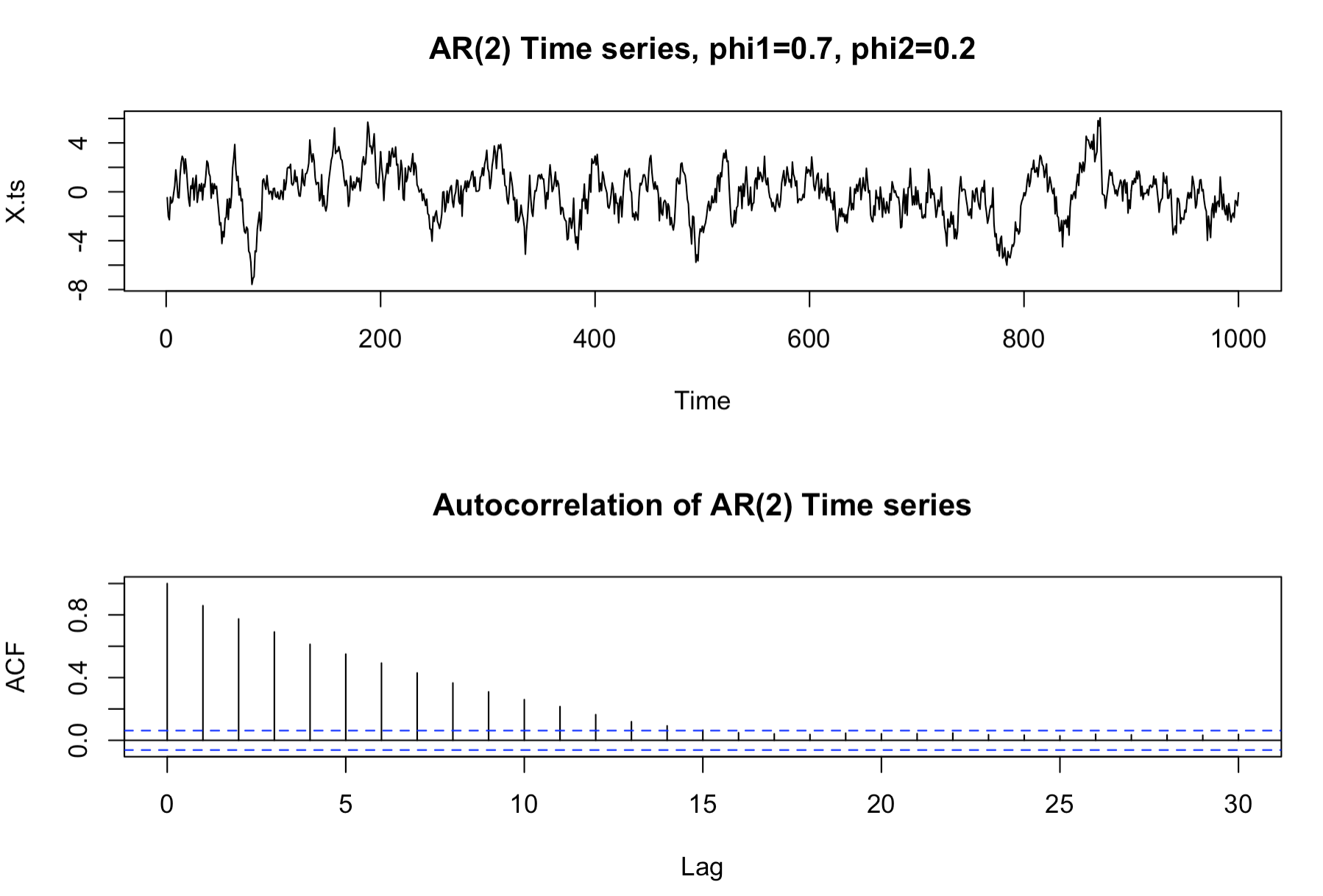
이를 R 코드로 구현하면 아래와 같다. 선차트를 통해 보면 현재 값이 과거 값과 높은 상관성이 있다는것을 확인할 수 있다. correlogram 을 통해 가까운 시간에 측정된 값이 현재값과 더 높은 상관성이 있다는것을 확인할 수 있다. (가중치가 0.7, 0.2 이므로)
set.seed(2017)
X.ts <- arima.sim(list(ar=c(0.7,0.2)), n=1000)
par(mfrow=c(2,1))
plot(X.ts, main="AR(2) Time series, phi1=0.7, phi2=0.2")
X.acf <- acf(X.ts, main="Autocorrelation of AR(2) Time series")
X.acf
Moving average process 와의 관계
Autoregressive process 는 moving average process 의 무한 수열로 나타낼 수 있다.
차수 (p) 가 1인 AR 을 생각해보자.
아래와 같이 식을 쓸 수 있다. (Z는 평균이 0, 분산이 sigma^2 을 따른다고 가정하고, phi 를 theta 로 치환하자.)
$$ X_t = Z_t + \phi X_{t-1} = Z_t + \phi Z_{t-1} + \phi^2 X_{t-2} ... = Z_t + \theta_1 Z_{t-1} + \theta_2 X_{t-2} ... $$
AR (1) 의 통계량
위와 같이 식을 써서 moving average 처럼 표현하면 AR process 에서의 X(t) 의 기댓값과 분산을 쉽게 구해볼 수 있다.
$$ E(X_t) = 0 $$
$$ V(X_t) = \sigma^2 \sum^{\infty}_{i=0}\theta_i^2 $$
time series 가 stationarity 를 만족하기 위해서는 분산이 t 에따라 바뀌지 않고, 일정해야한다. 그렇기 때문에 phi 의 절댓값이 1보다 작은것은 stationarity 에 대한 필요 조건이라고 할 수 있다.
AR(1) 의 auto covariance function
MA process 의 acf 와 유사한 형태라는것을 확인할 수 있다. (link)
$$ \gamma(k) = \sigma^2 \sum^{\infty}_{i=0} \theta_i \theta_{i+k} $$
AR(1) 의 auto correlation coefficient
$$ \rho(k) = \frac{\sum^{\infty}_{i=0} \theta_i \theta_{i+k}}{\sum^{\infty}_{i=0} \theta_i \theta_i} $$
theta 를 phi 로 치환하여 AR(1) 의 auto covariance 와 auto covariance coefficient 를 구해보자. (무한등비수열 공식 사용하여 정리)
$$ \gamma(k) = \sigma^2 \frac{\phi^k}{1-\phi^2} $$
$$ \rho(k) = \phi^k $$
AR Process 의 Stationarity 를 확인하는 방법
Example: AR(1) process
$$ X_t = Z_t + \phi X_{t-1} $$
위 AR(1) process 에서 Z 를 제외한 나머지 텀들을 한쪽으로 옮겨서 아래와 같은 식을 만들 수 있다.
$$ \phi(B) = 1-\phi B $$
이 때, 우변을 0으로 만드는 B 의 해를 찾는다. 해는 B = 1/phi 이다. B 의 해가 단위원 (unit circle) 바깥에 있는 것이 stationarity 를 만족하기 위한 조건이 된다. 따라서 AR(1) 모델에서는 phi 의 절댓값이 1 미만이어야 stationarity 를 만족한다.
Example: AR(2) process
$$ X_t = \frac{1}{3} X_{t-1} + \frac{1}{2} X_{t-2} + Z_t $$
$$ \phi(B) = 1-\frac{1}{3} B-\frac{1}{2} B^2 $$
위 식에서 B 의 해를 찾으면 (-2+sqrt(76))/6, (-2-sqrt(76))/6 이 된다. 위 두 값이 모두 단위원 바깥에 있기 때문에 위 AR(2) process 는 stationarity 를 만족한다.
'Data science > Statistics' 카테고리의 다른 글
| 충분 통계량의 기초 개념 (0) | 2023.12.12 |
|---|---|
| Maximum Likelihood Estimation 개념 정리 (0) | 2023.12.12 |
| 시계열분석 - Stationarity (0) | 2022.01.26 |
| 시계열분석 - Moving average process (0) | 2022.01.24 |
| 시계열분석 - Random walk (0) | 2022.01.24 |
